13 - TRIÂNGULOS

TRIÂNGULOS

Conceito: Triângulo é um polígono de três lados

Na figura acima:
= Os pontos A, B e C são vértices do triângulo.
= Os segmentos AB, BC e CA são os lados do triângulo.
= Os ângulos A, B e C são ângulos internos do triângulo

ÂNGULOS EXTERNO

Angulo externo é o ângulo suplementar do ângulo interno

PERÍMETRO

O perímetro de um  triângulo é igual à soma das medidas dos seus lados .

Perímetro ABC = AB + AC + BC



CLASSIFICAÇÃO DOS TRIÂNGULOS


Quanto aos lados os trângulos se classificam em:

= Equilátero quando tem os três lados congruentes.
= Isósceles quando tem dois lados congruentes
= Escaleno quando não temlados congruentes

Quanto aos ângulos os triângulos se classificam em:

= Acutângulo quando te três ângulos agudos
= Retângulo quando tem um ângulo reto.
= Obtusângulo quando tem um angulo obtuso

Em um triângulo retângulo os lados que formam o ângulo reto chamam-se catetos e o lado oposto ao ângulo reto chama-se hipotenusa.

EXERCÍCIOS

1) Observe o triângulo retangulo e responda:

a) Quais são os vértices?
b) Quais são os lados?
c) Quais são os ângulos?

2) O perimetro de um triângulo é 25 cm. Dois lados medem respectivamente 7,8 cm e 8,2 cm.  Calcule a medida do terceiro lado?

3) Determine o comprimento do lado BC, sabendo que o perímewtro do triângulo ABC é 48 cm.

4) O perímetro do triângulo ´34 cm . Determine o comprimento do menor lado.

5) Classifique o triângulo de acordo com as medidas dos lados.

6) Classifique o triângulo de acordo com as medidas dos ângulos ;

7) Observe a figura e responda:

a) Que nome recebe o lado BC?

b) Que nome recebem os lados AB e AC?


CONDIÇÕES DE EXISTÊNCIA DE UM TRIÂNGULO


Em qualquer triângulo, cada lado é menor que a soma dos outros dois lados

Exemplo

Vamos comparar a medida de cada lado com a soma das medidas dos outros dois
assim:

Para vferificar a citada propriedade, procure construir um triângulo com as seguintes medidas 7 cm, 4 cm e 2 cm .

È impossivel, não? Logo não existe o triângulo cujos lados, medem 7cm, 4cm e 2cm.

EXERCÍCIOS

1) Existe ou não um triângulo com lados medindo:

a) 10 cm , 8cm e 7cm?
b) 8cm, 4cm e 3 cm ?
c) 2cm, 4 cm e 6 cm?
d) 3 cm, 4 cm e 5 cm?
e) 3 cm, 5 cm e 6 cm?
f) 4 cm, 10 cm e 5cm?

2) Dois Lados de um triângulo isósceles medem 38 cm e 15 cm. Qual poderá ser a medida do terceiro lado?


ELEMENTOS NOTÁVEIS DE UM TRIÂNGULO

,= Mediana de um triângulo é o segmento que une um vértice ao ponto médio do lado oposto.

Todo triângulo tem três medianas que se encontram em um ponto chamado baricentro

Biossetriz de um triângulo é o segmento da bissetriz de um ângulo interno que tem por extremidades o vértice desse ângulo e o ponto de encontro com o lado oposto.

Todo triângulo tem três bissetrizes que se encontram em um ponto interior chamado incentro.

Altura de um triângulo é o segmento de perpendicular traçada de um vértice ao lado oposto ou ao seu prolongamento

Todo o trângulo tem três alturas que se encontram em um ponto chamado ortocentro

SOMA DAS MEDIDAS DOS ANGULOS INTERNOS DE UM TRIÂNGULO

Observe os triângulos e as medidas dos ângulos internos

vamos à demonstração desse teorema.

TEOREMA

Em qualquer triângulo, a soma das medidas dos ângulos internos é igual a 180°

Prova

EXERCÍCIOS RESOLVIDOS

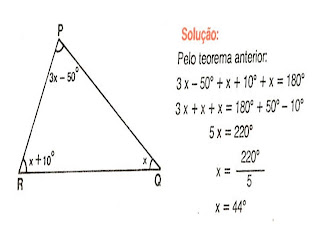
1) Calcular x no triângulo abaixo:

2) Calcule x no triângulo abaixo:

3) Calcule x no triângulo abaixo:

EXERCÍCIOS

1) Quanto vale a soma dos ângulos internos de um triângulo?

2) Copie e complete o quandro, sendo A,B e C ângulos internos de um triângulo.

3) Determine x em cada um dos triângulos

4) Determine x em cada um dos triângulos:

5) Determine a medida dos ângulos x, y e z.

TEOREMA DO ÂNGULO EXTERNO

Em qualquer triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não-adjacentes.

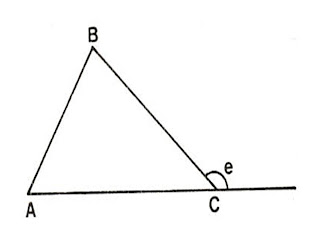
Prova:

consideremos um triângulo ABC. vamos provar que m(ê) = m(Â) + m (B) 

Exemplos

Calcule o valor de x no triângulo abaixo:

EXERCÍCIOS

1) Determine a medida do ângulo externo indicado em cada triângulo:

2) Calcule o valor de x nos triângulos dados:

3) Calcule o valor de x nos triângulos dados:

4) Calcule o valor de x nos triângulos dados:

5) Calcule o valor de x:

6) Calcule w e y :

7) Calcule x:

CONCRÊNCIA DE TRIÂNGULOS

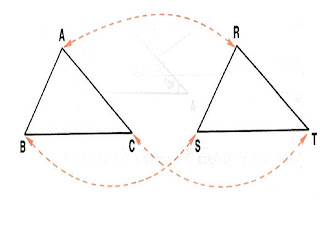
Intuitivamente, dois triângulos ABC e RST são congruentes se for possivel transportar um deles sobre o outro, de modo que eles coincidam.

Definição

Dois triângulos são chamados congruentes quando os lados e os angulos correspondentes são congruentes.

logo:

CASOS DE  CONGRUÊNCIA

O estudo dos casos de congruência de dois triângulos tem por finalidade estabelecer o menor número de condições para que dois triângulos sejam congruêntes.

1º CAS0 : L. L. L. ( lado, lado, lado)

Dois triângulos que têm os três lados respectivamente congruentes são congruentes.

2º CASO L. A. L. (lado, ângulo,  lado)

Dois treângulos que têm dois lados e o ângulo por eles formados respectivamente congruentes são con gruentes.

3º CASO A. L. A. ( ângulo, lado , ângulo)

Dois triângulos que tem um lado e dois ângulos adjacentes a esse lado respectivamente congruentes são congruentes.

4º CASO : L. A. A° ( lado , ângulo, ângulo oposto)

Dois trângulos que têm um lado, um ângulo adjacente e um ângulo oposto a esse lado respectivamente congruentes são congruentes.

EXERCÍCIOS

1) Cite, em cada item, o caso de congruência dos triângulos.